Customizing uitree nodes – part 2
Posted By Yair Altman On September 1, 2010 | 61 Comments
In my previous posts I have shown how Matlab’s semi-documented uitree and uitreenode functions can be used to display hierarchical (tree) control in Matlab GUI. Today I conclude this mini-series by answering a reader’s request [1] to show how checkboxes, radio buttons and other similar controls can be attached to tree nodes.
There are actually several ways this can be done:
Matlab icon control
The simplest is to create two icons (checked/unchecked) and switch the node’s icon whenever it is selected (use mtree’s NodeSelectedCallback or jtree’s MouseClickedCallback callbacks) – a sample implementation was posted by Gwendolyn Fischer [2] a couple of years ago, based on even earlier posts by John Anderson [3], Brad Phelan [4] and me. Here it is, with minor fixes:
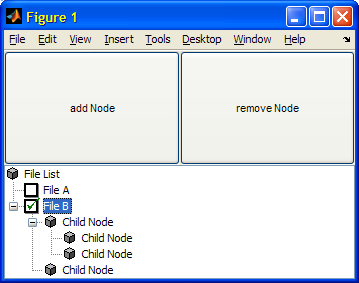
function uitree_demo
% function based on treeExperiment6 by John Anderson
% see https://www.mathworks.com/matlabcentral/newsreader/view_thread/104957#269485
%
% The mousePressedCallback part is inspired by Yair Altman
%
% derived from Brad Phelan's tree demo
% create a tree model based on UITreeNodes and insert into uitree.
% add and remove nodes from the treeModel and update the display
import javax.swing.*
import javax.swing.tree.*;
% figure window
f = figure('Units', 'normalized');
b1 = uicontrol( 'string','add Node', ...
'units' , 'normalized', ...
'position', [0 0.5 0.5 0.5], ...
'callback', @b1_cb);
b2 = uicontrol( 'string','remove Node', ...
'units' , 'normalized', ...
'position', [0.5 0.5 0.5 0.5], ...
'callback', @b2_cb);
%[I,map] = imread([matlab_work_path, '/checkedIcon.gif']);
[I,map] = checkedIcon;
javaImage_checked = im2java(I,map);
%[I,map] = imread([matlab_work_path, '/uncheckedIcon.gif']);
[I,map] = uncheckedIcon;
javaImage_unchecked = im2java(I,map);
% javaImage_checked/unchecked are assumed to have the same width
iconWidth = javaImage_unchecked.getWidth;
% create top node
rootNode = uitreenode('v0','root', 'File List', [], 0);
% [matlab_work_path, '/fileListIcon.gif'],0);
% create two children with checkboxes
cNode = uitreenode('v0','unselected', 'File A', [], 0);
% as icon is embedded here we set the icon via java, otherwise one could
% use the uitreenode syntax uitreenode(value, string, icon, isLeaf) with
% icon being a qualified pathname to an image to be used.
cNode.setIcon(javaImage_unchecked);
rootNode.add(cNode);
cNode = uitreenode('v0','unselected', 'File B', [], 0);
cNode.setIcon(javaImage_unchecked);
rootNode.add(cNode);
% set treeModel
treeModel = DefaultTreeModel( rootNode );
% create the tree
tree = uitree('v0');
tree.setModel( treeModel );
% we often rely on the underlying java tree
jtree = handle(tree.getTree,'CallbackProperties');
% some layout
drawnow;
set(tree, 'Units', 'normalized', 'position', [0 0 1 0.5]);
set(tree, 'NodeSelectedCallback', @selected_cb );
% make root the initially selected node
tree.setSelectedNode( rootNode );
% MousePressedCallback is not supported by the uitree, but by jtree
set(jtree, 'MousePressedCallback', @mousePressedCallback);
% Set the mouse-press callback
function mousePressedCallback(hTree, eventData) %,additionalVar)
% if eventData.isMetaDown % right-click is like a Meta-button
% if eventData.getClickCount==2 % how to detect double clicks
% Get the clicked node
clickX = eventData.getX;
clickY = eventData.getY;
treePath = jtree.getPathForLocation(clickX, clickY);
% check if a node was clicked
if ~isempty(treePath)
% check if the checkbox was clicked
if clickX <= (jtree.getPathBounds(treePath).x+iconWidth)
node = treePath.getLastPathComponent;
nodeValue = node.getValue;
% as the value field is the selected/unselected flag,
% we can also use it to only act on nodes with these values
switch nodeValue
case 'selected'
node.setValue('unselected');
node.setIcon(javaImage_unchecked);
jtree.treeDidChange();
case 'unselected'
node.setValue('selected');
node.setIcon(javaImage_checked);
jtree.treeDidChange();
end
end
end
end % function mousePressedCallback
function selected_cb( tree, ev )
nodes = tree.getSelectedNodes;
node = nodes(1);
path = node2path(node);
end
function path = node2path(node)
path = node.getPath;
for i=1:length(path);
p{i} = char(path(i).getName);
end
if length(p) > 1
path = fullfile(p{:});
else
path = p{1};
end
end
% add node
function b1_cb( h, env )
nodes = tree.getSelectedNodes;
node = nodes(1);
parent = node;
childNode = uitreenode('v0','dummy', 'Child Node', [], 0);
treeModel.insertNodeInto(childNode,parent,parent.getChildCount());
% expand to show added child
tree.setSelectedNode( childNode );
% insure additional nodes are added to parent
tree.setSelectedNode( parent );
end
% remove node
function b2_cb( h, env )
nodes = tree.getSelectedNodes;
node = nodes(1);
if ~node.isRoot
nP = node.getPreviousSibling;
nN = node.getNextSibling;
if ~isempty( nN )
tree.setSelectedNode( nN );
elseif ~isempty( nP )
tree.setSelectedNode( nP );
else
tree.setSelectedNode( node.getParent );
end
treeModel.removeNodeFromParent( node );
end
end
end % of main function treeExperiment6
function [I,map] = checkedIcon()
I = uint8(...
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0;
2,2,2,2,2,2,2,2,2,2,2,2,2,0,0,1;
2,2,2,2,2,2,2,2,2,2,2,2,0,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,0,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,0,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,0,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,0,0,1,1,2,2,3,1;
2,2,1,0,0,1,1,0,0,1,1,1,2,2,3,1;
2,2,1,1,0,0,0,0,1,1,1,1,2,2,3,1;
2,2,1,1,0,0,0,0,1,1,1,1,2,2,3,1;
2,2,1,1,1,0,0,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,0,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,1;
2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,1;
1,3,3,3,3,3,3,3,3,3,3,3,3,3,3,1]);
map = [0.023529,0.4902,0;
1,1,1;
0,0,0;
0.50196,0.50196,0.50196;
0.50196,0.50196,0.50196;
0,0,0;
0,0,0;
0,0,0];
end
function [I,map] = uncheckedIcon()
I = uint8(...
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1;
2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1;
2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,1,1,1,1,1,1,1,1,1,1,2,2,3,1;
2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,1;
2,2,2,2,2,2,2,2,2,2,2,2,2,2,3,1;
1,3,3,3,3,3,3,3,3,3,3,3,3,3,3,1]);
map = ...
[0.023529,0.4902,0;
1,1,1;
0,0,0;
0.50196,0.50196,0.50196;
0.50196,0.50196,0.50196;
0,0,0;
0,0,0;
0,0,0];
end
Custom Java classes
An alternative is to create a custom tree Java class and/or a custom TreeCellRenderer [5]/TreeCellEditor [6]. Specifically, to change the icons of each node you have to implement your own java component which derives from DefaultMutableTreeNode [7].
Some online resources to get you started:
- Sun’s official JTree customization tutorial [8]
- Santhosh Kumar’s custom tree icons [9], tree-node checkboxes [10], and selective tree-node checkboxes [11]
- Java2s’s multiple JTree customization snippets [12]
Built-in classes
Another option is to use Matlab’s built-in classes, either com.mathworks.mwswing.checkboxtree.CheckBoxTree or com.jidesoft.swing.CheckBoxTree:
import com.mathworks.mwswing.checkboxtree.*
jRoot = DefaultCheckBoxNode('Root');
l1a = DefaultCheckBoxNode('Letters'); jRoot.add(l1a);
l1b = DefaultCheckBoxNode('Numbers'); jRoot.add(l1b);
l2a = DefaultCheckBoxNode('A'); l1a.add(l2a);
l2b = DefaultCheckBoxNode('b'); l1a.add(l2b);
l2c = DefaultCheckBoxNode('α'); l1a.add(l2c);
l2d = DefaultCheckBoxNode('β'); l1a.add(l2d);
l2e = DefaultCheckBoxNode('3.1415'); l1b.add(l2e);
% Present the standard MJTree:
jTree = com.mathworks.mwswing.MJTree(jRoot);
jScrollPane = com.mathworks.mwswing.MJScrollPane(jTree);
[jComp,hc] = javacomponent(jScrollPane,[10,10,120,110],gcf);
% Now present the CheckBoxTree:
jCheckBoxTree = CheckBoxTree(jTree.getModel);
jScrollPane = com.mathworks.mwswing.MJScrollPane(jCheckBoxTree);
[jComp,hc] = javacomponent(jScrollPane,[150,10,120,110],gcf);
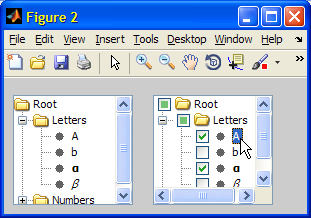
Note: Matlab’s CheckBoxTree does not have a separate data model. Instead, it relies on the base MJTree’s model, which is a DefaultTreeModel [13] by default. JIDE’s CheckBoxTree does have its own model.
This concludes my uitree mini-series. If you have any special customizations, please post a comment below [14].
Categories: GUI, Icons, Java, Medium risk of breaking in future versions, Semi-documented function
61 Comments (Open | Close)
Article printed from Undocumented Matlab: https://undocumentedmatlab.com
URL to article: https://undocumentedmatlab.com/articles/customizing-uitree-nodes-2
URLs in this post:
[1] request: http://undocumentedmatlab.com/blog/customizing-uitree/#comment-15781
[2] Gwendolyn Fischer: https://www.mathworks.com/matlabcentral/newsreader/view_thread/164189#416971
[3] John Anderson: https://www.mathworks.com/matlabcentral/newsreader/view_thread/104957#269485
[4] Brad Phelan: http://web.archive.org/web/20071015115312/xtargets.com/cms/Tutorials/Matlab-Programming/Handle-Graphics-Tree-Control-With-Nested-Functions.html
[5] TreeCellRenderer: http://download.oracle.com/javase/6/docs/api/javax/swing/tree/DefaultTreeCellRenderer.html
[6] TreeCellEditor: http://download.oracle.com/javase/6/docs/api/javax/swing/tree/DefaultTreeCellEditor.html
[7] DefaultMutableTreeNode: http://download.oracle.com/javase/6/docs/api/javax/swing/tree/DefaultMutableTreeNode.html
[8] JTree customization tutorial: http://java.sun.com/docs/books/tutorial/uiswing/components/tree.html
[9] custom tree icons: http://www.jroller.com/santhosh/entry/coloring_icons
[10] tree-node checkboxes: http://www.jroller.com/santhosh/entry/jtree_with_checkboxes
[11] selective tree-node checkboxes: http://www.jroller.com/santhosh/entry/show_checkboxes_only_on_specific
[12] JTree customization snippets: http://www.java2s.com/Code/Java/Swing-JFC/Tree.htm
[13] DefaultTreeModel: http://download.oracle.com/javase/6/docs/api/javax/swing/tree/DefaultTreeModel.html
[14] below: http://undocumentedmatlab.com/blog/customizing-uitree-nodes-2/#respond
[15] Customizing uitree nodes – part 1 : https://undocumentedmatlab.com/articles/customizing-uitree-nodes
[16] Customizing uitree : https://undocumentedmatlab.com/articles/customizing-uitree
[17] An interesting uitree utility : https://undocumentedmatlab.com/articles/interesting-uitree-utility
[18] uitree : https://undocumentedmatlab.com/articles/uitree
[19] Adding a context-menu to a uitree : https://undocumentedmatlab.com/articles/adding-context-menu-to-uitree
[20] Customizing menu items part 3 : https://undocumentedmatlab.com/articles/customizing-menu-items-part-3
[21] : https://undocumentedmatlab.com/blog/tri-state-checkbox/
[22] : https://undocumentedmatlab.com/blog/customizing-uitree-nodes/
[23] : https://undocumentedmatlab.com/blog/uicontrol-callbacks/#memory_leak
[24] : https://undocumentedmatlab.com/blog/adding-context-menu-to-uitree/
[25] : https://undocumentedmatlab.com/blog/customizing-uitree-nodes
[26] : https://undocumentedmatlab.com/blog/customizing-uitree-nodes-2
[27] : http://docs.oracle.com/javase/7/docs/api/javax/swing/tree/DefaultTreeCellRenderer.html
Click here to print.
61 Comments To "Customizing uitree nodes – part 2"
#1 Comment By Mikhail On September 2, 2010 @ 04:30
I prefer pure Java solution and then putting JPanel containing JTree into MATLAB figure using javacomponent(). I used code from http://www.javaspecialists.eu/archive/Issue145.html
#2 Comment By Amy On September 2, 2010 @ 11:57
This is great. Is there a way to apply a filter to display only certain file types when using the tree for a file system?
#3 Comment By Yair Altman On September 2, 2010 @ 12:17
@Mikhail – the link you posted is to a TristateCheckBox class, not a CheckBox tree. I plan to write an article someday about Matlab’s internal tri-state checkbox classes. Being internal and available in Matlab out-of-the-box, they are more useful than 3rd-party classes.
@Amy – filters are not available by default in uitree, but you can trap the node expansion callback function to implement this relatively easily.
#4 Comment By Yair Altman On October 27, 2011 @ 13:51
@Mikhail – as promised, I posted the [21] last week.
It took me over a year from your comment, but I guess that it is better late than never, right?
#5 Comment By KK On September 5, 2010 @ 14:22
Thanks for your great entry. I really like jave based checkbox tree.
Do you know how to callback in java based checkbox tree?
#6 Comment By Scott Koch On October 5, 2010 @ 15:11
Thanks again for the great post. I’ve been playing with jtrees a lot lately and could now really use some customization of the Drag and Drop behavior. So, here’s a vote for a post on DnD.
Thanks
Scott
#7 Comment By Alex On December 7, 2010 @ 09:46
How do I get the information which checkboxes are checked when I use com.mathworks.mwswing.checkboxtree.CheckBoxTree?
#8 Comment By Alex On December 8, 2010 @ 06:11
Found a solution:
#9 Comment By Rex On August 2, 2011 @ 21:20
this is amazing!
i have a question about how to hide the Root.
just like a file system directory, use this method i can just display the files in C:\, how to show the files in D:\ within the same tree?
#10 Comment By Yair Altman On August 3, 2011 @ 00:12
@Rex – I’m not sure you can using a simple single command: “My Computer” is not really a valid system folder. However, you can setup two tree nodes, one for C:\ and the other for D:\, and display them in a uitree. It’s not as simple as a one-line command, but it’s not very difficult and it will do what you want.
#11 Comment By Rex On August 7, 2011 @ 00:27
hi,Yair
I am an antenna engineer. I want to design a GUI to manage my antenna pattern data.
I realized a tree i need with actxcontrol about 4 years ago. This tree inluced some icons, i integrate them with a ActvieX Dll design with visual basic to load the pictures. But according to your blog, i think using VBScript to load the image is more effective.
Now i want to design a tree with uitree, but i do not know how to make them within one tree:
Root1
|__Child11
| |_____Subchild111
| |_____Subchild112
|__Child12
|_____Subchild121
|_____Subchild122
Root2
|__Child21
| |_____Subchild211
| |_____Subchild212
|__Child22
|_____Subchild221
|_____Subchild222
#12 Comment By Yair Altman On September 18, 2011 @ 17:00
@Rex – the [22] described how to create a custom tree.
#13 Comment By Amjad Elshenawy On September 18, 2011 @ 05:05
Hi Yair,
We have used ‘com.jidesoft.swing.CheckBoxTree’
We want to have callback for two different user actions, namely,
– Checkbox checking event and
– Mouse click on the string without checking the check box itself
For the first event, we managed to handle it using the following lines of code
However for the second event we did not manage to find a listener.
Please advise
Thanks in advance
Amjad
#14 Comment By Yair Altman On September 18, 2011 @ 16:56
@Amjad – there are several callbacks that you can use – all of them directly on the
jCheckBoxTreeobject. Specifically, your best guess would probably be MouseClickedCallback. Also, take a look at the related ClickInCheckBoxOnly boolean property.#15 Comment By Mark On February 13, 2014 @ 03:57
Hi Yair and Amjad,
It cannot be stressed enough: thanks for this wonderful website! It truly is of great help in my daily struggle with MATLAB gui controls 🙂
I know this post was from some time ago, but perhaps you can help me with a minor callback issue I face now. I have created a CheckBoxTree using Yair’s second approach (using the built-in classes from com.mathworks.mwswing.checkboxtree.CheckBoxTree). I would like to take action after selection or deselection of an item in the tree.
Setting the ValueChangedCallback does not seem to work, since that callback only triggers when the item focus has changed (so checking and immediately unchecking the same item trigger the ValueChangedCallback only once; R2013a). The MouseClickedCallback works perfectly (albeit only with selection by mouse, not by the space bar of course). However, if I set the callback like this:
set( jCheckBoxTree, 'MouseClickedCallback', 'disp(''test'')' );Matlab generates a warning:
Is there a way: (1) to set the callback function more elegantly, so that the warning is not shown anymore, or (2) suppress the warning (I don’t know the message identifier).
Thanks in advance!
With kind regards,
Mark
#16 Comment By Yair Altman On February 13, 2014 @ 04:22
@Mark – use the handle() wrapper. See [23]
#17 Comment By Mark On February 13, 2014 @ 06:44
Thanks!
#18 Pingback By Tri-state checkbox | Undocumented Matlab On October 19, 2011 @ 07:07
[…] I have already described a built-in Matlab tree control whose nodes have tri-state checkboxes […]
#19 Comment By Jerome Lecoq On December 28, 2012 @ 13:23
Hi Yair,
First, thank you so much for your entire website. This is a real bible for making interfaces in Matlab.
I am using uitree in one of my program and everything you posted about is working. I am trying to be able to draw a rectangle on the tree to select multiple nodes (like what you can do on the listbox). I was wondering if there was a simple Java property to change to allow this that you were aware of. I can’t find it.
Thanks!
#20 Comment By Yair Altman On December 29, 2012 @ 08:40
@Jerome – you can use ctrl-click to select multiple nodes. I’m not sure about a bounding box (you can probably find a solution in one of the numerous java forums/websites)
#21 Comment By Domenico Reggio On February 23, 2013 @ 05:04
Hello Yair,
great to follow all your postings, even if I have difficulties to understand the details of connections/interface between Java and Matlab.
Now I am trying to add ToolTips to an uitree node/leaf. As you proposed I true to use to manipulate the renderer with the Tooltip manager. But I am not able to continue. Do you have some tips for me? This is my code
I read somewhere that I need to reach the following:
public class JTreeExample extends JFrame { public JTreeExample() { JTree tree = new JTree(); tree.setCellRenderer(new MyRenderer()); ToolTipManager.sharedInstance().registerComponent(tree); } private class MyRenderer extends DefaultTreeCellRenderer { @Override public Component getTreeCellRendererComponent(JTree tree, Object value, boolean sel, boolean expanded, boolean leaf, int row, boolean hasFocus) { JLabel component = (JLabel) super.getTreeCellRendererComponent( tree, value, sel, expanded, leaf, row, hasFocus); component.setToolTipText("tooltip !!! "); return component; } } public static void main(String[] args) { new JTreeExample(); } }Thanks a lot!
Best Regards,
Domenico
#22 Comment By Yair Altman On February 23, 2013 @ 16:06
@Domenico – you need to create a dedicated Java cell renderer class, compile it using a Java compiler, and then set your tree to the new class. If you’re not comfortable with Java, you can use a workaround such as the one that I’ve shown for [24].
#23 Comment By Yishai E On April 1, 2013 @ 15:25
Hi Yair,
I’m trying to make a tree lazily expand based on a very complicated data model that I have already coded (a bunch of classes that are built in a tree). The expansion of every node depends on the data that the node contains, and I store this data in the UserData field of the uitreenode.
To invoke the right node expansion subfunction, I need access to this field *of the node I am expanding*. This works fine when I double click the node I want to expand:
selNode = tree.getSelectedNodes; NodeData = selNode.handle.UserData; if isa(NodeData, 'CLASS_1'), nodes = fExpandCLASS_1_Node(tree, value, NodeData); elseif isa(NodeData, 'CLASS_2'), nodes = fExpandCLASS_2_Node(tree, value, NodeData); else nodes = []; endHowever, if I just click the [+] icon, the expansion function gets called but the node isn’t selected. How can get the node that is being expanded in the callback? I couldn’t find any function in the Jtree or the UITreePeer that would do that for me.
Also, I don’t think I can make any use of ‘value’ because in my implementation it’s just a string (I can’t cast my classes into handles; or can I?).
#24 Comment By Yair Altman On April 1, 2013 @ 15:31
@Yishai – place your code in a function and attach this function to the uitree’s NodeExpandedCallback. This callback function gets the node handle in the second input parameter.
Note that uitree‘s help section (in uitree.m) incorrectly calls the property ExpandedFcn, whereas the correct name is NodeExpandedCallback. If you make this change, you can use the example in the help section to see a sample node-expansion callback function.
#25 Comment By Yishai E On April 1, 2013 @ 23:00
OK, I think I got it. This morning I explored every single field in the tree and found that this works:
Hope someone finds this helpful.
#26 Comment By Yishai E On April 1, 2013 @ 23:13
Thanks Yair,
I didn’t see your reply when I posted. I guess both solutions work, but I already had everything written this way so I stuck to it, just changed the way I get to the UserData field.
Thanks again,
Yishai
#27 Comment By Keming On April 18, 2013 @ 02:37
Hello Yair,
I have created two matlab GUIs, GUI A has a tree view by using uitree and GUI B has a button which be able to modify the tree view in the GUI A. But the problem is that the GUI B can not get uitree handle by using general passing data method among GUIs.
The following code in GUI A
handles.archit=uitreenode('v0','Lecture','Lecture',[],false); handles.archit.add(uitreenode('v0','Math1','Further Math',[],true)); [handles.archit_tree, archit_container]=uitree('v0','Root',handles.archit,'Position',[-1,0,187,234]);The following code in GUI B
h=findobj('Tag','GUI_A'); handle=guihandles(h); handle.archit.add(uitreenode('v0','Urburnel','Urburnel',[],true)); handle.archit_tree.reloadNode(handle.cycle);Looking forward to your reply!
Thanks!
Kind regards,
Keming
#28 Comment By Yair Altman On April 18, 2013 @ 02:42
@Keming – you can store all the handles using setappdata and then retrieve those handles using getappdata
#29 Comment By Keming On April 24, 2013 @ 18:24
Yair, Thank you for your help, you are always right!
#30 Comment By Natalie On October 23, 2013 @ 12:17
I was hoping you could help with an issue i’ve been having. I created the tree perfectly fine, but how can you determine (either during or after the fact) that a checkbox was selected? I have played around with the callbacks but the only one i could get to work (‘ValueChangedCallback’) fires only when the name is clicked on, not the checkbox. How can i tell if the checkbox is clicked? Is there an event for it? I’ve been using the ‘methodsview’ function in matlab to try and figure it out with little helpful return…
One other other comments mentioned a ‘l1a.getSelectionState’ which gives me an error of ‘???No appropriate method or public field getSelectionState for class com.mathworks.mwswing.checkboxtree.CheckBoxTree’
Also, i am creating the tree inside a for loop, since it must be dynamic based on different data. There wasn’t any way i could see of moving through the tree in matlab (such as starting at the root, moving to the housed nodes, etc.) which i thought i could possibly use and determine each checked state individually…but cannot.
help?
Thank you in advance.
#31 Comment By Yair Altman On October 24, 2013 @ 02:41
@Natalie – I don’t have an immediate answer, but I’m pretty sure that it can be done using a combination of properties/callbacks. If you’d like me to spend some time to investigate and solve this for you (for a small consulting fee), please contact me by email.
#32 Comment By Richard A On April 7, 2014 @ 04:41
I have a super basic question here. I’m very new to Java but have been working with MATLAB and its vanilla flavor GUIs for 10+ years.
My goal is to create an interactive plotting tool to display waveforms depending on if its node is checked or not.
In the uitree_demo under the function mousePressedCallback, we find the following line of code:
For my kludged together tree, this is what is returned:
I see that this contains all of the information I am after (it tells me which node has been clicked) but I am at a loss as to how to get at it. I would love it if I could get a MATLAB structure or even a string of the above treePath. So, how do you suggest to do this and where can I go to read up on how to do this right?
Thanks.
#33 Comment By Richard A On April 7, 2014 @ 05:00
Found a kludge for my problem
Now, I can parse the string with regular expressions. Please point me to a better way.
#34 Comment By Yair Altman On April 7, 2014 @ 05:01
@Richard –
#35 Comment By B. Kline On July 23, 2014 @ 07:24
Quick question I hope. I have a that built off a folder structure, and anytime the user inputs a new file I’m deleting the uitree and creating it again using the uitree(‘v0′,’Root’,'[directorypath],handle.panel) method. However this causes me to have to expand through the tree and set some custom icons and also have to do alot of leg work to put the tree in the same state collapse wise. Is there any easy way to update the tree so that if new files/folder exists they are just there and I dont have to create it new everytime?
Thanks in advance, and thanks for this site and the Book.
#36 Comment By Yair Altman On July 25, 2014 @ 11:59
You can add/remove specific nodes in run-time. See the [25] of this series, or in my book (section 4.2) for details.
#37 Comment By David On September 2, 2014 @ 23:44
Hi Yair,
Do you know of a way to save the checkbox tree? I have created a very large tree in my application and I would like to load it from a file each time rather than having to re-create. It appears that the nodes cannot be serialized during save.
Example:
node = com.mathworks.mwswing.checkboxtree.DefaultCheckBoxNode(‘test’);
save(‘test’, ‘node’);
#38 Comment By Yair Altman On September 2, 2014 @ 23:47
you’ll need to programmatically save the tree’s data model
#39 Comment By kpmandani On September 8, 2014 @ 13:01
Can you tell me what code should be written to find file location. I have created a CheckBoxTree using Yair’s second approach (using the built-in classes from com.mathworks.mwswing.checkboxtree.CheckBoxTree). Also suggest me where it should be added inside that code.
#40 Comment By kpmandani On September 10, 2014 @ 06:44
I am using example of [26] ‘built in classes’ example. I am using it because I want tick as per how it is mentioned in the output of that code. Now if I want to get file location using the same format I am unable to do so. I did try with slight editing in the words (instead of tree I wrote JTree as the example code uses ‘JTree’ and not just ‘tree’)..
selectedNodes = tree.getSelectedNodes; nodePath = selectedNodes(1).getPath.cell; subPathStrs = cellfun(@(p) [p.getName.char,filesep],nodePath,’un’,0); pathStr = strrep([subPathStrs{:}], [filesep,filesep],filesep);But it gives me error as
No appropriate method, property, or field getSelectedNodes for class com.mathworks.mwswing.MJTree.
Error in
selectedNodes = jTree.getSelectedNodes;
Can you tell me where I am going wrong?
#41 Comment By Yair Altman On September 10, 2014 @ 06:50
kpmandi – I already suggested that you contact me by email for paid consulting. Please stop posting questions here again and again. This is my website, it is NOT a general Q&A forum.
#42 Pingback By CheckboxList | Undocumented Matlab On September 10, 2014 @ 11:02
[…] Several years ago I blogged about using a checkbox-tree in Matlab. A few days ago there was a question on the Matlab Answers forum asking whether something similar […]
#43 Comment By Alexander On September 12, 2014 @ 02:11
Hello, first off all thanks for the great Work.
I am using the CheckBoxTree as explained above. But iam not sure how the tree is actually working and couldnt find any helpful informations on other sites.
myCode:
How can i update the tree after initializing? Is the jTree or jCheckBoxTree my main object? jCheckBoxTree.expandPath(..) works for me.
Since i am using CheckBoxTree, your information about the uitree doesnt seem to help.
Thanks a lot
#44 Comment By Alexander On September 12, 2014 @ 02:26
Seems like i found the solution. For everybody with the same problem, this solves the problem:
But i am still not able to delete the root node. Neither
jCheckBoxTree.removeAllnorjCheckBoxTree.removeSelectionPath(nodeRoot)works for me.#45 Comment By Masoud On March 9, 2015 @ 12:18
hi master
I would define a number of pushbutton or table ,… For each node on the figuer
When i change node ,chenge the information on the figuer like table or chekbox
#46 Comment By Sebastian On March 12, 2015 @ 07:45
I have been looking into the Matlab implementation of the CheckBoxTree (
com.mathworks.mwswing.checkboxtree.CheckBoxTree). The problem I’m facing is that whenever I click the Label (e.g. like in the last figure of the article, where “A” is clicked), the state of according checkbox also changes.I would expect the following behaviour:
1) Click label -> MouseClickedCallback is fired
2) Click CheckBox -> Change State of CheckBox -> MouseClickedCallback is fired
What steps do I need to take to prevent the CheckBox from getting changed when clicking the label?
#47 Comment By Yair Altman On March 12, 2015 @ 07:58
@Sebastian – I assume that you can get the click location from the callback’s eventData parameter, and thereby decide whether or not to rever the checkbox state. Or maybe there’s an option in one of the object’s properties to modify this behavior.
#48 Comment By michael r On August 27, 2015 @ 04:52
Hi
If I using DefaultCheckBoxNode to create CheckBoxTree and I want to change the icon of the leaf and still having the checkbox on it. How do I do it ?
#49 Comment By Yair Altman On September 18, 2015 @ 04:38
@Michael – this requires modifying the [27]. I explain cell-renderers in my Matlab-Java book, but here is a short example:
jTree = com.mathworks.mwswing.MJTree(jRoot); jTreeCR = jTree.getCellRenderer; icon = javax.swing.ImageIcon('C:\icons\leaf.gif'); jTreeCR.setLeafIcon(icon);#50 Comment By Daniel On March 30, 2016 @ 14:59
Hi there!
I just created a tree using ui.extras.jTree and I need to count the number of nodes under each parent node. There seem to be no method corresponding to getChildCount() as in JTree. Any help or tips?
#51 Comment By Yair Altman On April 21, 2016 @ 13:00
@Daniel – try to use the parent’s Children property, as in:
numel(hParent.Children)#52 Comment By ACenTe On April 18, 2016 @ 19:14
Hello Yair.
First of all, great article.
I need to create a CheckBoxTree using com.mathworks.mwswing.checkboxtree.CheckBoxTree. However, I need to customize the icons and when changing the CellRenderer in the original MJTree, changes don’t apply to the CheckBoxTree.
Could you please tell me how can I achieve this? I tried modifying the CheckBoxTree’s CellRenderer, but it says that there’s no ‘setLeafIcon’ for CheckBoxTreeCellRenderer.
Thank you in advance for your help.
#53 Comment By Yair Altman On April 21, 2016 @ 12:56
@ACenTe – this would probably require creating a custom CellRenderer class in Java. Email me for private consulting on this if you are interested.
#54 Comment By KhRaIf On April 20, 2016 @ 17:47
Hi Yair,
A big respect for you and your website. Really helpfull!
I have a question regarding the uitree/uitreenode and if it is possible to speed up the process. I have built my tree using uitreenode, and the user can have several filters. Because I have more then 1e4 elements, it takes quite a while filter everytime. For the time being, I do it using the following workflow:
this is taking too much time.
Is there a possibility to speed up things? Maybe by extracting a small tree from a larger tree?
Thanks in advance,
#55 Comment By Yair Altman On April 21, 2016 @ 13:05
@KhRaIf – there are several ways in which you can speed up your Matlab code. In general, you need to run the Profiler and see where the performance hotspot is, and try to optimize that. One general idea that could help is to create the tree model first, and only then to attach it to the tree, rather than updating a visible tree one node at a time (which is much slower since the tree needs to refresh after each update). Also, updating an invisible tree is faster than a visible one – you can make it visible when it is ready.
If you still need additional assistance, email me for private consulting.
#56 Comment By Andreas Horn On April 29, 2017 @ 18:10
Dear Yair,
this is an incredibly cool resource as all your stuff.
I’m using the
com.mathworks.mwswing.checkboxtree.DefaultCheckBoxNodeand would like to set the state of the check boxes programmatically.I know the getSelectionState property that works fine for me.
However, setSelectionState method does not:
Any ideas?
Thanks so much!
#57 Comment By Andreas Horn On April 29, 2017 @ 18:56
… found a solution:
However, this unfortunately does not update the parent selection boxes. Is there any method to re-validate the whole selection state of the jtree?
Thanks so much!
#58 Comment By Paul M. On October 20, 2017 @ 20:26
Excellent tutorial,
I am using the Matlab built in class (com.mathworks.mwswing.checkboxtree.CheckBoxTree), how do I get a list of which nodes have the check box marked?
If I use:
…from the built-in class example I get a list of the highlighted nodes, not the checked ones.
-Thanks
#59 Comment By Yair Altman On October 22, 2017 @ 09:39
@Paul – you can check each node’s SelectionState property value, and you can compare it to
com.mathworks.mwswing.checkboxtree.SelectionState.SELECTED,.NOT_SELECTEDor.MIXED. For example:#60 Comment By Yuriy On May 30, 2019 @ 14:26
Hello!! Please help me deal with the matlab. You have a very useful article, but is it possible to implement setting the flag in the tree for uifigure using javacomponent or uitree ???
#61 Comment By Yair Altman On May 31, 2019 @ 04:05
Yuriy – I do not understand your question