Speeding-up builtin Matlab functions – part 3

A recurring theme in this website is that despite a common misperception, builtin Matlab functions are typically coded for maximal accuracy and correctness, but not necessarily best run-time performance. Despite this, we can often identify and fix the hotspots in these functions and use a modified faster variant in our code. I have shown multiple examples for this in various posts (example1, example2, many others).

Today I will show another example, this time speeding up the mvksdensity (multi-variate kernel probability density estimate) function, part of the Statistics toolbox since R2016a. You will need Matlab R2016a or newer with the Stats Toolbox to recreate my results, but the general methodology and conclusions hold well for numerous other builtin Matlab functions that may be slowing down your Matlab program. In my specific problem, this function was used to compute the probability density-function (PDF) over a 1024×1024 data mesh.

The builtin mvksdensity function took 76 seconds to run on my machine; I got this down to 13 seconds, a 6x speedup, without compromising accuracy. Here’s how I did this:

Preparing the work files

While we could in theory modify Matlab’s installed m-files if we have administrator privileges, doing this is not a good idea for several reasons. Instead, we should copy and rename the relevant internal files to our work folder, and only modify our local copies.

To see where the builtin files are located, we can use the which function:

>> which('mvksdensity')
C:\Program Files\Matlab\R2020a\toolbox\stats\stats\mvksdensity.m

In our case, we copy \toolbox\stats\stats\mvksdensity.m as mvksdensity_.m to our work folder, replace the function name at the top of the file from mvksdensity to mvksdensity_, and modify our code to call mvksdensity_ rather than mvksdensity.

If we run our code, we get an error telling us that Matlab can’t find the statkscompute function (in line #107 of our mvksdensity_.m). So we find statkscompute.m in the \toolbox\stats\stats\private\ folder, copy it as statkscompute_.m to our work folder, rename its function name (at the top of the file) to statkscompute_, and modify our mvksdensity_.m to call statkscompute_ rather than statkscompute:

[fout,xout,u] = statkscompute_(ftype,xi,xispecified,npoints,u,L,U,weight,cutoff,...

We now repeat the process over and over, until we have all copied all the necessary internal files for the program to run. In our case, it tuns out that in addition to mvksdensity.m and statkscompute.m, we also need to copy statkskernelinfo.m.

Finally, we check that the numeric results using the copied files are exactly the same as from the builtin method, just to be on the safe side that we have not left out some forgotten internal file.

Now that we have copied these 3 files, in practice all our attentions will be focused on the dokernel sub-function inside statkscompute_.m, since the profiling report (below) indicates that this is where all of the run-time is spent.

Identifying the hotspots

Now we run the code through the Matlab Profiler, using the “Run and Time” button in the Matlab Editor, or profile on/report in the Matlab console (Command Window). The results show that 99.8% of mvksdensity‘s time was spent in the internal dokernel function, 75% of which was spent in self-time (meaning code lines within dokernel):

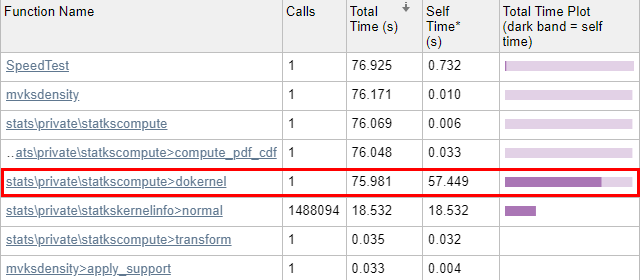
Let’s drill into dokernel and see where the problems are:

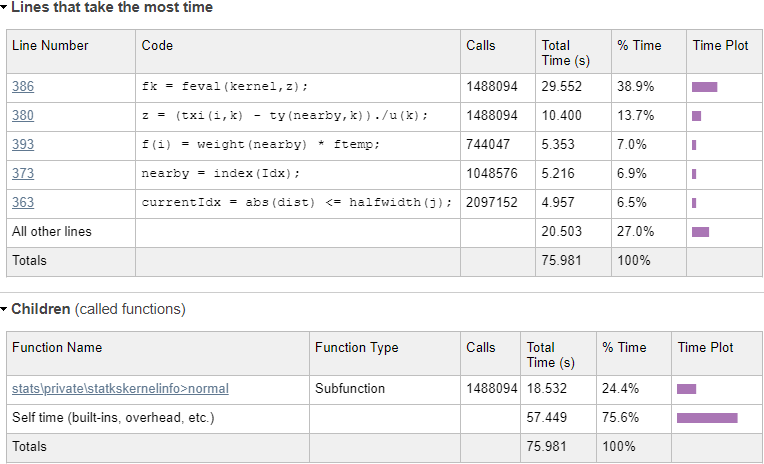
Evaluating the normal kernel distribution

We can immediately see from the profiling results that a single line (#386) in statkscompute_.m is responsible for nearly 40% of the total run-time:

fk = feval(kernel,z);

In this case, kernel is a function handle to the normal-distribution function in \stats\private\statkskernelinfo>normal, which is evaluated 1,488,094 times. Using feval incurs an overhead, as can be seen by the difference in run-times: line #386 takes 29.55 secs, whereas the normal function evaluations only take 18.53 secs. In fact, if you drill into the normal function in the profiling report, you’ll see that the actual code line that computes the normal distribution only takes 8-9 seconds – all the rest (~20 secs, or ~30% of the total) is totally redundant function-call overhead. Let’s try to remove this overhead by calling the kernel function directly:

fk = kernel(z);

Now that we have a local copy of statkscompute_.m, we can safely modify the dokernel sub-function, specifically line #386 as explained above. It turns out that just bypassing the feval call and using the function-handle directly does not improve the run-time (decrease the function-call overhead) significantly, at least on recent Matlab releases (it has a greater effect on old Matlab releases, but that’s a side-issue).

We now recognize that the program only evaluates the normal-distribution kernel, which is the default kernel. So let’s handle this special case by inlining the kernel’s one-line code (from statkskernelinfo_.m) directly (note how we move the condition outside of the loop, so that it doesn’t get recomputed 1 million times):

...
isKernelNormal = strcmp(char(kernel),'normal');  % line #357 for i = 1:m
    Idx = true(n,1);
    cdfIdx = true(n,1);
    cdfIdx_allBelow = true(n,1);
    for j = 1:d
        dist = txi(i,j) - ty(:,j);
        currentIdx = abs(dist) <= halfwidth(j);
        Idx = currentIdx & Idx; % pdf boundary
        if iscdf
            currentCdfIdx = dist >= -halfwidth(j);
            cdfIdx = currentCdfIdx & cdfIdx; %cdf boundary1, equal or below the query point in all dimension
            currentCdfIdx_below = dist - halfwidth(j) > 0;                   
            cdfIdx_allBelow = currentCdfIdx_below & cdfIdx_allBelow; %cdf boundary2, below the pdf lower boundary in all dimension
        end
    end
    if ~iscdf
        nearby = index(Idx);
    else
        nearby = index((Idx|cdfIdx)&(~cdfIdx_allBelow));
    end
    if ~isempty(nearby)
        ftemp = ones(length(nearby),1);
        for k =1:d
            z = (txi(i,k) - ty(nearby,k))./u(k);
            if reflectionPDF
                zleft  = (txi(i,k) + ty(nearby,k)-2*L(k))./u(k);
                zright = (txi(i,k) + ty(nearby,k)-2*U(k))./u(k);
                fk = kernel(z) + kernel(zleft) + kernel(zright);  % old: =feval()+...
            elseif isKernelNormal                fk = exp(-0.5 * (z.*z)) ./ sqrt(2*pi);            else
                fk = kernel(z);  %old: =feval(kernel,z);            end
            if needUntransform(k)
                fk = untransform_f(fk,L(k),U(k),xi(i,k));
            end
            ftemp = ftemp.*fk;
        end
        f(i) = weight(nearby) * ftemp;
    end
    if iscdf && any(cdfIdx_allBelow)
        f(i) = f(i) + sum(weight(cdfIdx_allBelow));
    end
end
...

This reduced the kernel evaluation run-time from ~30 secs down to 8-9 secs. Not only did we remove the direct function-call overhead, but also the overheads associated with calling a sub-function in a different m-file. The total run-time is now down to 45-55 seconds (expect some fluctuations from run to run). Not a bad start.

Main loop – bottom part

Now let’s take a fresh look at the profiling report, and focus separately on the bottom and top parts of the main loop, which you can see above. We start with the bottom part, since we already messed with it in our fix to the kernel evaluation:

The first thing we note is that there’s an inner loop that runs d=2 times (d is set in line #127 of mvksdensity_.m – it is the input mesh’s dimensionality, and also the number of columns in the txi data matrix). We can easily vectorize this inner loop, but we take care to do this only for the special case of d==2 and when some other special conditions occur.

In addition, we hoist outside of the main loop anything that we can (such as the constant exponential power, and the weight multiplication when it is constant [which is typical]), so that they are only computed once instead of 1 million times:

...
isKernelNormal = strcmp(char(kernel),'normal');
anyNeedTransform = any(needUntransform);uniqueWeights = unique(weight);isSingleWeight = ~iscdf && numel(uniqueWeights)==1;isSpecialCase1 = isKernelNormal && ~reflectionPDF && ~anyNeedTransform && d==2;expFactor = -0.5 ./ (u.*u)';TWO_PI = 2*pi;for i = 1:m
    ...
    if ~isempty(nearby)
        if isSpecialCase1            z = txi(i,:) - ty(nearby,:);            ftemp = exp((z.*z) * expFactor);        else            ftemp = 1;  % no need for the slow ones()            for k = 1:d
                z = (txi(i,k) - ty(nearby,k)) ./ u(k);
                if reflectionPDF
                    zleft  = (txi(i,k) + ty(nearby,k)-2*L(k)) ./ u(k);
                    zright = (txi(i,k) + ty(nearby,k)-2*U(k)) ./ u(k);
                    fk = kernel(z) + kernel(zleft) + kernel(zright);  % old: =feval()+...
                elseif isKernelNormal
                    fk = exp(-0.5 * (z.*z)) ./ sqrt(TWO_PI);
                else
                    fk = kernel(z);  % old: =feval(kernel,z)
                end
                if needUntransform(k)
                    fk = untransform_f(fk,L(k),U(k),xi(i,k));
                end
                ftemp = ftemp.*fk;
            end
            ftemp = ftemp * TWO_PI;
        end        if isSingleWeight            f(i) = sum(ftemp);        else            f(i) = weight(nearby) * ftemp;
        end    end
    if iscdf && any(cdfIdx_allBelow)
        f(i) = f(i) + sum(weight(cdfIdx_allBelow));
    end
end
if isSingleWeight    f = f * uniqueWeights;endif isKernelNormal && ~reflectionPDF    f = f ./ TWO_PI;end...

This brings the run-time down to 31-32 secs. Not bad at all, but we can still do much better:

Main loop – top part

Now let’s take a look at the profiling report’s top part of the main loop:

Again we note is that there’s an inner loop that runs d=2 times, which we can again easily vectorize. In addition, we note the unnecessary repeated initializations of the true(n,1) vector, which can easily be hoisted outside the loop:

...
TRUE_N = true(n,1);isSpecialCase2 = ~iscdf && d==2;for i = 1:m
    if isSpecialCase2        dist = txi(i,:) - ty;        currentIdx = abs(dist) <= halfwidth;        currentIdx = currentIdx(:,1) & currentIdx(:,2);        nearby = index(currentIdx);    else        Idx = TRUE_N;        cdfIdx = TRUE_N;        cdfIdx_allBelow = TRUE_N;        for j = 1:d
            dist = txi(i,j) - ty(:,j);
            currentIdx = abs(dist) <= halfwidth(j);
            Idx = currentIdx & Idx; % pdf boundary
            if iscdf
                currentCdfIdx = dist >= -halfwidth(j);
                cdfIdx = currentCdfIdx & cdfIdx; % cdf boundary1, equal or below the query point in all dimension
                currentCdfIdx_below = dist - halfwidth(j) > 0;
                cdfIdx_allBelow = currentCdfIdx_below & cdfIdx_allBelow; %cdf boundary2, below the pdf lower boundary in all dimension
            end
        end
        if ~iscdf
            nearby = index(Idx);
        else
            nearby = index((Idx|cdfIdx)&(~cdfIdx_allBelow));
        end
    end    if ~isempty(nearby)
        ...

This brings the run-time down to 24 seconds.

We next note that instead of using numeric indexes to compute the nearby vector, we could use faster logical indexes:

...
%index = (1:n)';  % this is no longer neededTRUE_N = true(n,1);
isSpecialCase2 = ~iscdf && d==2;
for i = 1:m
    if isSpecialCase2
        dist = txi(i,:) - ty;
        currentIdx = abs(dist) <= halfwidth;
        nearby = currentIdx(:,1) & currentIdx(:,2);    else
        Idx = TRUE_N;
        cdfIdx = TRUE_N;
        cdfIdx_allBelow = TRUE_N;
        for j = 1:d
            dist = txi(i,j) - ty(:,j);
            currentIdx = abs(dist) <= halfwidth(j);
            Idx = currentIdx & Idx; % pdf boundary
            if iscdf
                currentCdfIdx = dist >= -halfwidth(j);
                cdfIdx = currentCdfIdx & cdfIdx; % cdf boundary1, equal or below the query point in all dimension
                currentCdfIdx_below = dist - halfwidth(j) > 0;
                cdfIdx_allBelow = currentCdfIdx_below & cdfIdx_allBelow; %cdf boundary2, below the pdf lower boundary in all dimension
            end
        end
        if ~iscdf
            nearby = Idx;  % not index(Idx)        else
            nearby = (Idx|cdfIdx) & ~cdfIdx_allBelow;  % no index()        end
    end
    if any(nearby)        ...

This brings the run-time down to 20 seconds.

We now note that the main loop runs m=1,048,576 (=1024×1024) times over all rows of txi. This is expected, since the loop runs over all the elements of a 1024×1024 mesh grid, which are reshaped as a 1,048,576-element column array at some earlier point in the processing, resulting in a m-by-d matrix (1,048,576-by-2 in our specific case). This information helps us, because we know that there are only 1024 unique values in each of the two columns of txi. Therefore, instead of computing the “closeness” metric (which leads to the nearby vector) for all 1,048,576 x 2 values of txi, we calculate separate vectors for each of the 1024 unique values in each of its 2 columns, and then merge the results inside the loop:

...
isSpecialCase2 = ~iscdf && d==2;
if isSpecialCase2    [unique1Vals, ~, unique1Idx] = unique(txi(:,1));    [unique2Vals, ~, unique2Idx] = unique(txi(:,2));    dist1 = unique1Vals' - ty(:,1);    dist2 = unique2Vals' - ty(:,2);    currentIdx1 = abs(dist1) <= halfwidth(1);    currentIdx2 = abs(dist2) <= halfwidth(2);endfor i = 1:m
    if isSpecialCase2
        idx1 = unique1Idx(i);        idx2 = unique2Idx(i);        nearby = currentIdx1(:,idx1) & currentIdx2(:,idx2);    else
        ...

This brings the run-time down to 13 seconds, a total speedup of almost ~6x compared to the original version. Not bad at all.

For reference, here’s a profiling summary of the dokernel function again, showing the updated performance hotspots:

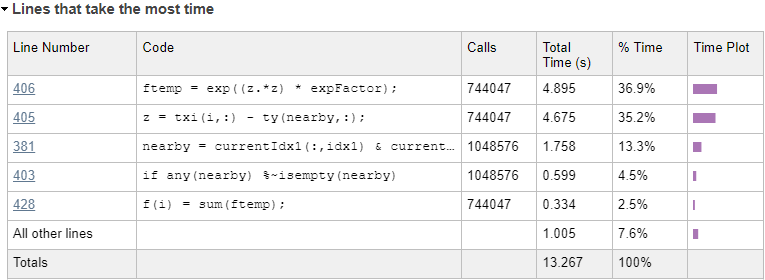
The 2 vectorized code lines in the bottom part of the main loop now account for 72% of the remaining run-time:

    ...
    if ~isempty(nearby)
        if isSpecialCase1
            z = txi(i,:) - ty(nearby,:);            ftemp = exp((z.*z) * expFactor);        else
            ...

If I had the inclination, speeding up these two code lines would be the next logical step, but I stop at this point. Interested readers could pick up this challenge and post a solution in the comments section below. I haven’t tried it myself, so perhaps there’s no easy way to improve this. Then again, perhaps the answer is just around the corner – if you don’t try, you’ll never know…

Data density/resolution

So far, all the optimization I made have not affected code accuracy, generality or resolution. This is always the best approach if you have some spare coding time on your hands.

In some cases, we might have a deep understanding of our domain problem to be able to sacrifice a bit of accuracy in return for run-time speedup. In our case, we identify the main loop over 1024×1024 elements as the deciding factor in the run-time. If we reduce the grid-size by 50% in each dimension (i.e. 512×512), the run-time decreases by an additional factor of almost 4, down to ~3.5 seconds, which is what we would have expected since the main loop size has decreased 4 times in size. While this reduces the results resolution/accuracy, we got a 4x speedup in a fraction of the time that it took to make all the coding changes above.

Different situations may require different approaches: in some cases we cannot sacrifice accuracy/resolution, and must spend time to improve the algorithm implementation; in other cases coding time is at a premium and we can sacrifice accuracy/resolution; and in other cases still, we could use a combination of both approaches.

Conclusions

Matlab is composed of thousands of internal functions. Each and every one of these functions was meticulously developed and tested by engineers, who are after all only human. Whereas supreme emphasis is always placed with Matlab functions on their accuracy, run-time performance often takes a back-seat. Make no mistake about this: code accuracy is almost always more important than speed, so I’m not complaining about the current state of affairs.

But when we run into a specific run-time problem in our Matlab program, we should not despair if we see that built-in functions cause slowdown. We can try to avoid calling those functions (for example, by reducing the number of invocations, or decreasing the data resolution, or limiting the target accuracy, etc.), or we could optimize these functions in our own local copy, as I have shown today. There are multiple techniques that we could employ to improve the run time. Just use the profiler and keep an open mind about alternative speed-up mechanisms, and you’d be half-way there. For ideas about the multitude of different speedup techniques that you could use in Matlab, see my book Accelerating Matlab Performance.

Let me know if you’d like me to assist with your Matlab project, either developing it from scratch or improving your existing code, or just training you in how to improve your Matlab code’s run-time/robustness/usability/appearance.

In the meantime, Happy Easter/Passover everyone, and stay healthy!